Video: Qual è la formula di Eulero che usa il numero di facce del tetraedro con vertici come 4 e 6 bordi?
2024 Autore: Stanley Ellington | [email protected]. Ultima modifica: 2023-12-16 00:19
Questa pagina elenca le prove del formula di Eulero : per qualsiasi poliedro convesso, il numero di vertici e facce insieme è esattamente due in più del numero di bordi . Simbolicamente V-E+F=2. Per esempio, a tetraedro ha quattro vertici , quattro facce e sei bordi ; 4 - 6 + 4 =2.
Di conseguenza, quale sarà il numero di facce se ci sono 6 vertici e 12 spigoli?
Un cubo o un parallelepipedo è una forma tridimensionale che ha 12 bordi , 8 angoli o vertici , e 6 facce.
Ci si potrebbe anche chiedere, come funziona la formula di Eulero? La formula di Eulero , Uno dei due importanti teoremi matematici di Leonhard Eulero . Il primo è un'invarianza topologica (vedi topologia) relativa al numero di facce, vertici e bordi di qualsiasi poliedro. Si scrive F + V = E + 2, dove F è il numero di facce, V il numero di vertici ed E il numero di spigoli.
qual è la formula per la relazione tra il numero di facce vertici e spigoli di un cubo?
V - E + F = 2; o, in parole: the numero di vertici , meno il numero di bordi , più il numero di facce , è uguale a Due.
Qual è la formula del poliedro di Eulero?
Questo teorema implica La formula poliedrica di Eulero (a volte chiamato La formula di Eulero ). Oggi diremmo questo risultato come: Il numero di vertici V, facce F e spigoli E in un convesso tridimensionale poliedro , soddisfa V + F - E = 2.
Consigliato:
Il numero di serie è lo stesso del numero VIN di una casa mobile?
1) C'è un adesivo di carta all'interno di tutte le case mobili prodotte dal giugno del 1976, chiamato "targhetta dati", che elenca il numero VIN (chiamato anche numero di serie), insieme ad altri fatti sulla fabbricazione della casa . Il VIN sarà chiamato il numero di serie del produttore sulla targhetta dati
Come si esprime un numero decimale ripetuto con una serie infinita?
Un decimale ripetuto è un decimale le cui cifre si ripetono. Una serie geometrica infinita è una serie di numeri che va avanti all'infinito che ha lo stesso rapporto costante tra tutti i numeri successivi. Tutti i decimali ripetuti possono essere riscritti come una serie geometrica infinita di questa forma: a + ar + ar2 + ar3 +
Quale nome è stato dato al crollo di Wall Street del 29 ottobre 1929 noto anche come il crollo del mercato azionario del 1929 che portò alla Grande Depressione negli anni '30 la Grande Depressione era un mondo grave
La Grande Depressione iniziò negli Stati Uniti dopo un forte calo dei prezzi delle azioni che iniziò intorno al 4 settembre 1929 e divenne notizia mondiale con il crollo del mercato azionario del 29 ottobre 1929 (noto come Martedì Nero). Tra il 1929 e il 1932, il prodotto interno lordo (PIL) mondiale è diminuito di circa il 15%
Qual è il numero P e il numero di gruppo?
Metalli di base: il numero P Questo numero viene utilizzato per raggruppare metalli di base simili, consentendo la qualificazione di un'intera selezione rispetto alla qualificazione di una sola. Questi metalli di base sono raggruppati per materiale e assegnati numeri P in base a quale materiale sono
Come si moltiplica un numero misto per un numero intero?
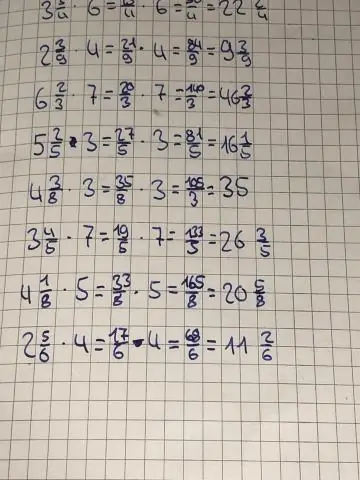
Moltiplicazione di un numero misto e un numero intero Il numero misto viene convertito in una frazione impropria e il numero intero viene scritto come frazione con denominatore. Si esegue la moltiplicazione delle frazioni e, se necessario, la semplificazione. La frazione risultante è scritta come un numero misto nella forma più semplice